LCM & HCF Previous Year Questions PDF & Study Notes: The full forms of L.C.M. and H.C.F. are the Least Common Multiple and Highest Common factor, respectively. The H.C.F. defines the greatest factor present in between given two or more numbers, whereas L.C.M. defines the least number which is exactly divisible by two or more numbers.

The number system constitutes an important part of the Quantitative Aptitude section. We are providing notes on the topic “HCF & LCM” with previous year questions asked in various exams like SSC & Railway. Also, we will solve some problems based on these two concepts to understand them better.

LCM & HCF Previous Year Questions PDF: Overview

Chapter Name	LCM & HCF
Category	Study Materials
Covers	LCM & HCF Concepts, Formulae, Examples, Short Tricks & Previous Year Questions
Useful For	SSC, Banking, Railways, State PCS, UPSC, Other Competetive Exams & Interview
Language	Hindi + English
Total Number Of Questions	500+
Format	PDF
Quality	Best
Status	Released
Compiled By	www.www.examstocks.com

LCM And HCF Definition

Least Common Multiple (LCM)

In arithmetic, the least common multiple or LCM of two numbers say a and b, is denoted as LCM (a,b). And the LCM is the smallest or least positive integer that is divisible by both a and b.

Multiple: Multiple is the product of any quantity and an integer.

Common Multiple: Common multiple is that which is multiple of two or more numbers. The common multiples of 2 and 3 are 0, 6,12,18, 24, etc.

Example: LCM of 5 and 6 = 30 because 30 is the smallest multiple which is common to 5 and 6 (Or we can say that 30 is the smallest number which is divisible by both 5 and 6).

Highest Common Factor (HCF)

As the rules of mathematics dictate, the greatest common divisor or the gcd of two or more positive integers happens to be the largest positive integer that divides the numbers without leaving a remainder.

Factor: Numbers that are multiplied together to get another number are called factors of that number. e.g. 3 and 4 are factors of 12, because 3 × 4 = 12. A number can have many factors.

Common factors: Factors that are common to two or more numbers are called common factors.

How to find LCM and HCF?

Here are the methods we can use to find the HCF and LCM of given numbers.

1. Prime factorization method
2. Division method

Let us learn both methods one by one.

Factorization or prime numbers method to Find LCM:

• Step 1: Express each number as a product of prime factors.
• Step 2: LCM is the product of the highest powers of all prime factors

Example 1: Find out LCM of 8 and 14

Step 1: Express each number as a product of prime factors.
8 = 23
14 = 2 × 7

Step 2: LCM is the product of the highest powers of all prime factors
Here the prime factors are 2 and 7
The highest power of 2 here = 2³
The highest power of 7 here = 7
Hence LCM = 2³ × 7 = 56

Division Method to Find LCM (Shortcut):

• Step 1: Write the given numbers in a horizontal line separated by commas.
• Step 2: Divide the given numbers by the smallest prime number which can exactly divide at least two of the given numbers.
• Step 3: Write the quotients and undivided numbers in a line below the first.
• Step 4: Repeat the process until we reach a stage where no prime factor is common to any two numbers in the row.
• Step 5: LCM is the product of all the divisors and the numbers in the last line.
  e.g. Find the LCM of 20, 25, and 30 by long division method.

Factorization or prime numbers method of finding HCF:

• Step 1: Express each number as a product of prime factors.
• Step 2: HCF is the product of all common prime factors using the least power of each common prime factor.

e.g. Find the HCF of 27 and 36

27 = 3³
36 = 3² x 2²

Find the HCF of 108, 288, and 360.
108 = 2² x 3³
288 = 2⁵ x 3²
360 = 2³ x 5 x 3²
HCF = 2² x 3² = 36

Division Method to find HCF (Shortcut):

• Step 1: Divide the larger number by the smaller number
• Step 2: Divisor of step 1 is divided by its remainder
• Step 3: The divisor of step 2 is divided by its remainder. Continue this process till we get 0 as the remainder.
• Step 4: The divisor of the last step is the HCF.

e.g. Find the HCF of 108 and 288.

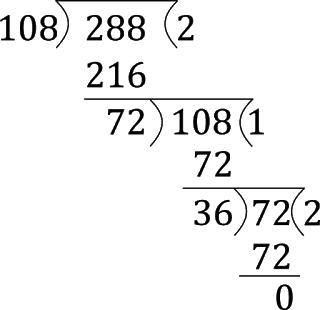
LCM and HCF Of Decimals and Fractions

LCM of decimals:

Make the decimal place the same in all the given numbers, find the LCM as they are integers, and adjust the decimal accordingly in the final result.

e.g. Find the LCM of 0.6, 9.6 and 0.36

Solution:
numbers can be written as, 0.60, 9.60 and .36
now find the LCM of 60, 960, and 36, which is 2880.
Adjust the decimal accordingly, i.e. 28.80

LCM of Fractions:

The LCM of two or more fractions is the least fraction or integer which is exactly divisible by each of them.

LCM = (LCM of Numerators) / (HCF of denominators)

Note:
Product of two numbers = Product of their HCF and LCM
HCF of numbers always divides LCM exactly.

HCF of decimals:

Make the decimal place the same in all the given numbers, find the HCF as they are integers, and adjust the decimal accordingly in the final result.

e.g Find the HCF of 16.5, 0.45, and 15.

Solution:
numbers can be written as, 16.50, 0.45 and 15.00
now find the HCF of 1650, 45, and 1500, which is 15.
Adjust the decimal accordingly, i.e. 0.15

HCF of Fractions:

The HCF of two or more fractions is the highest fraction which is exactly divisible by each of the fractions.

HCF = (HCF of Numerators) / (LCM of denominators)

LCM and HCF Formula

The formula which involves both HCF and LCM is:

Product of Two numbers = (HCF of the two numbers) x (LCM of the two numbers)

Say, A and B are the two numbers, then as per the formula;

A x B = H.C.F.(A,B) x L.C.M.(A,B)
We can also write the above formula in terms of HCF and LCM, such as:

• H.C.F. of Two numbers = Product of Two numbers/L.C.M of two numbers
• L.C.M of two numbers = Product of Two numbers/H.C.F. of Two numbers

LCM and HCF Question And Answers PDF

Here we have shared some questions and answers based on LCM and HCF which were asked in previous year exams of SSC and Railways. You can try to solve these questions by using above mentioned methods and comment down your answers.

Q1. The LCM of two numbers is 1920 and their HCF is 16. If one of the numbers is 128, find the other number.

(a) 204
(b) 240
(c) 260
(d) 320

Q2. The HCF and product of two numbers are 15 and 6300 respectively. The number of possible pairs of the numbers is:

(a) 4
(b) 3
(c) 2
(d) 1

Q3. The LCM of the two numbers is 4 times their HCF. The sum of LCM and HCF is 125. If one of the numbers is 100, then the other number is:

(a) 5
(b) 25
(c) 100
(d) 125

Q4. The HCF and LCM of the two numbers are 13 and 455 respectively. If one of the numbers lies between 75 and 125, then, that numbers are:

(a) 78
(b) 91
(c) 104
(d) 117

Q5. The least number, which when divided by 12, 15, 20, or 54 leaves a remainder of 4 in each case, is:

(a) 450
(b) 454
(c) 540
(d) 544

Q6. Find the greatest number of five digits which when divided by 3, 5, 8, 12 have 2 as a reminder:

(a) 99999
(b) 99958
(c) 99960
(d) 99962

Q7. The least number which when divided by 16, 18, 20, and 25 leaves 4 as a remainder in each case but when divided by 7 leaves no remainder is:

(a) 17004
(b) 18000
(c) 18002
(d) 18004

Q8. What is the least number which when divided by the numbers 3, 5, 6, 8, 10, and 12 leaves in each case a remainder 2 but when divided by 13 leaves no remainder?

(a) 312
(b) 962
(c) 1562
(d) 1586

Q9. The traffic lights at three different road crossings change after 24 seconds, 36 seconds, and 54 seconds respectively. If they all change simultaneously at 10:15:00 AM, then at what time will they again change simultaneously?

(a) 10:16:54 AM
(b) 10:18:36 AM
(c) 10:17:02 AM
(d) 10:22:12 AM

Q10. From a point on a circular track 5 km long A, B and C started running in the same direction at the same time with the speed of 2(1/2) km per hour, 3 km per hour, and 2 km per hour respectively. Then on the starting point, all three will meet again after:

(a) 30 hours
(b) 6 hours
(c) 10 hours
(d) 15 hours

Q11. Let N be the greatest number that will divide 1305, 4665, and 6905 leaving the same remainder in each case. Then, the sum of the digits in N is:

(a) 4
(b) 5
(c) 6
(d) 8

Q12. Three sets of English, Mathematics and Science books containing 336, 240, 96 books respectively have to be stacked in such a way that all the books are stored subject-wise and the height of each stack is the same. The total number of stacks will be:

(a) 14
(b) 21
(c) 22
(d) 48

Q13. Three numbers are in the ratio 2: 3: 4 and their H.C.F. is 12. The L.C.M. of the numbers is:

(a) 144
(b) 192
(c) 96
(d) 72

Q14. The H.C.F and L.C.M. of two numbers are 21 and 84 respectively. If the ratio of the two numbers is 1: 4, then the larger of the two numbers is:

(a) 12
(b) 108
(c) 48
(d) 84

Q15. The number between 3000 and 4000 which is exactly divisible by 30, 36, and 80 is:

(a) 3625
(b) 3250
(c) 3500
(d) 3600

LCM and HCF Study Materials PDF

Download SSC Previous Year LCM HCF Questions PDF

Download LCM HCF Previous Year Questions PDF

Download LCM HCF Handwritten Notes PDF For Competitive Exams

Frequently Asked Questions

Q. What are the LCM and HCF?
Ans. – The H.C.F. defines the greatest factor present in between given two or more numbers, whereas L.C.M. defines the least number which is exactly divisible by two or more numbers.

Q. What is the HCF of 24 and 36?
Ans. – Common Factors of 24 and 36: 1, 2, 3, 4, 6, 8, and 12. since 12 is the biggest common factor for 24 and 36. it is the HCF of 24 and 36.

Q. What is the relationship between LCM and HCF?
Ans. – The product of LCM and HCF of the given natural numbers is equivalent to the product of the given numbers.

Q. What is the full form of GCF?
Ans. – GCF stands for Greatest Common Factor.